
| NASLOVNICA | Zašto istraživati Mars? | XVI. st. | XVII. st. | XVIII. st. | XIX. st. |
| Mariner | Viking | Mars Global Surveyour | Mars Pathfinder | Mars Polar Lander |
| Kon? Zakon! | UFOlogija | Art |

|
Kakvi su ljudi kompjutori:
|
U istom radu Turing navodi i argumente protiv mogućnosti da strojevi uspješno simuliraju mišljenje. U nastavku su svi navedeni zato jer je većina od njih i danas vrlo aktualna:
 1) Teološki argument ;
Mišljenje je funkcija čovjekove besmrtne duše.
Bog je dao besmrtnu dušu ljudima, ali ne životinjama
ili strojevima. Otud strojevi ne mogu misliti.
1) Teološki argument ;
Mišljenje je funkcija čovjekove besmrtne duše.
Bog je dao besmrtnu dušu ljudima, ali ne životinjama
ili strojevima. Otud strojevi ne mogu misliti.
2) Argument "glave u pijesku" ; Posljedice strojnog
mišljenja bile bi previše opasne. Zato se nadajmo i
vjerujmo da strojevi ne mogu misliti.
Ova dva gore navedena argumenta Turing ne smatra previše
vrijednima da se o njima puno diskutira.
3) Matematički argument ; Razni dokazi ukazali su
na ograničenja snage diskretnih strojeva. To su rezultati
Godela, Churcha, Turinga i drugih. Nedvojbeno je, dakle da postoje
stvari koje strojevi ne mogu učiniti. Drugim riječima,
za svaki stroj se može pronaći problem koji on ne
može riješiti. Ali zato se može konstruirati drugi
stroj koji taj problem može riješiti, ali ne može
riješiti neki drugi itd. Osim toga ovaj argument se temelji
na nedokazanoj činjenici da ograničenja koja vrijede
za strojeve ne vrijede za ljudski um. Je li to tako, još
se ne može reći, ali i ljudi sami često griješe
i daju pogrešne odgovore.
4) Argument svijesti ; Po ovom argumentu strojevi ne mogu
pisati sonete ili komponirati, jer nemaju emocije i nemaju znanje
o tome da su nešto napisali. Ni jedan mehanizam ne može
osjetiti radost uspjeha, ljutnju, tugu, itd.
Po Turingu, doslovno gledajući, solipsistički, ne
možemo biti ni sigurni da opisane doživljaje može
itko imati osim nas samih. O iskustvima tuđih doživljaja
znamo samo ono što čujemo u komunikaciji. Nije nemoguće
napraviti stroj koji će nas konzistentno izvještavati
o "svojim doživljajima". Postoji podosta nejasnoća
oko problema svijesti i taj problem se još istražuje.
No, ne treba zato unaprijed tvrditi da je ona osnovni preduvjet
za mišljenje.
5) Argument o različitim nemogućnostima ; Ako
se i napravi stroj koji radi sve spomenute stvari, on nikad neće
moći raditi X. Pod X se uklapa čitav niz aktivnosti
poput: ljubaznosti, prijateljstva, imati inicijativu, imati smisao
za humor, činiti greške, zaljubiti se, uživati
u jagodama s tučenim vrhnjem, itd.
Turing prvo obrazlaže da ljudi imaju predodžbe o strojevima
sudeći prema onima s kojima su se su susretali. Vjerojatno
bi se mogli napraviti strojevi koji bi obavljali ili simulirali
navedene aktivnosti. Ali, npr. što će nam stroj koji
uživa u jagodama s tučenim vrhnjem. To što stoj
ne može pokazati ili simulirati cjelokupnu raznovrsnost
ljudskog ponašanja nije problem apsolutne nemogućnosti
stroja, već, po Turingu, ograničenja kapaciteta
stroja poput memorije i brzine, ali nedostatka potrebe da se
tako složen i dugotrajan posao uopće počne
raditi.
6) Argument Lady Lovelace ; Lady Lovelace bila je kći
lorda Byrona i prvi programer namijenjen za Babbageov Analitički
Stroj. Ona je rekla da takav stroj može izvesti sve što
znamo odrediti kako da se izvede. Dakle, on ne može napraviti
ništa novo, već samo ono što mu je određeno
da radi.
Turing smatra da bi se ovaj problem mogao riješiti ako na
pravilan način uspijemo programirati strojeve da uče.
Osim toga, takvu vrstu programiranja Turing smatra izuzetno važnom
u nastojanju da se naprave programi koji su kadri izvoditi inteligentne
aktivnosti.
7) Argument o kontinuiranosti živčanog sustava ;
Istina je da stroj diskretnih stanja mora biti različit
od kontinuiranog stroja i po tome je različit od ljudskog
mozga. Ali, po Turingu diskretni strojevi mogu simulirati odgovore,
tj. davati vrlo približne odgovore onima koje bi davao diferencijalni
analizator.
8) Argument o neformalnosti ponašanja ; Ne postoje
formalna pravila za ljudskog ponašanja. Kada bi se ljudsko
ponašanje moglo opisati pravilima značilo bi da smo
mi neka vrsta strojeva. Budući da to nije tako, mi smo
različiti od strojeva. Po Turingu, to što još
nisu nađena pravila ponašanja ne znače da ona
ne postoje. Možda su presložena, a možda se i
ne istražuju na sve adekvatne načine.
9) Argument iz ekstrasenzorne percepcije (ukoliko ona postoji)
; Kako bi stroj simulirao aktivnost osobe obdarene telepatijom?
Ovo je jedini argument na koji Turing ne daje zadovoljavajući
odgovor.
Poznati primjer suprotnog stajališta od Turingovog je onaj iznesen u Lucasovom (1961) radu i ustvari se odnosi na treći Turingov argument ; matematički argument. On rezonira na slijedeći način: Godelov teorem se mora primijeniti na strojeve zato što se on radi o samoj biti stroja koji je konkretna izvedba formalnog sustava (za koje teorem ustvari vrijedi). Slijedi da je za bilo koji dani stroj postoji formula koja je nedokaziva u sustavu. Koliko god složeni stroj konstruiramo dodavanjem novih pravila uvijek će postojati nešto što stroj neće moći napraviti, a ljudski um može. Otud Lucas zaključuje da ni jedan stroj ne može biti adekvatan model uma, i da su umovi po svojoj biti različiti od strojeva. Nadalje, izneseno je i da stroj ne može dokazati istinitost o vlastitoj konzistenciji, dok um koji nije stroj to može. Kao primjer za to Lucas navodi ljudsku samo-svjesnost kao dokaz o konzistentnosti ljudskog ima, te tvrdi da stroj nikad neće moći postići samo-svjesnost. Na kraju, navodi da je moguće konstruirati mehaničke modele uma, ali ni jedan neće biti kompletno adekvatan i dorečen.
Na ovom mjestu mogu se iznesti i Hofstadterovi (1980) protuargumenti
na ovu Lucasovu tezu.
1) Naime, ako tvrdimo da ne možemo napisati program koji
će moći uvijek primijeniti operaciju "godeliziranja"
(tj. primijeniti Godelovu metodu) znači da ni mi sami
to ne možemo napraviti u svakom slučaju. Po Hofstadteru,
Lucas čini pogrešku izjednačavajući
apstraktnu mogućnost "godeliziranja", i znanja
kako da se to učini u svakom pojedinačnom slučaju.
Ako ni mi ne možemo eksplicitno reći što je uključeno
u primjeni Godelove metode u svim slučajevima, tada će
za svakog od nas vjerojatno doći do tako složenog
slučaja da nećemo znati kako da primijenimo tu metodu.
2) Drugi, možda jasniji argument koji navodi Hofstadter
je da su ljudi podjednako podložni Godelovom teoremu kada
se on prevede u riječi. Radi se o varijacijama Empedoklovog
paradoksa. Imamo jedan lijepi primjer, a to je slijedeća
rečenica:
"Lucas ne može konzistentno potvrditi OVU rečenicu."
Ako pažljivo promotrimo ovu rečenicu možemo
vidjeti da
a) ona je istinita, a ipak
b) Lucas ju ne može konzistentno potvrditi.
Dakle, i Lucas i bilo koji drugi čovjek (jer se za svakog
može naći odgovarajuća rečenica) nisu
cjeloviti sustavi, jer postoji istinita rečenica čiju
istinitost on ne može potvrditi.
3) Lucas također pretpostavlja da je stroj konkretna izvedba
formalnog sustava. To doista i jest tako na razini hardvera.
Međutim, on čini pogrešku smatrajući da
je to jedina razina na kojoj se odvija manipulacija simbolima.
No, to nije tako. Štoviše, istraživanja u umjetnoj
inteligenciji razvila su brojne programe koji mogu manipulirati
slikama, formulirati analogije, zaboravljati, miješati pojmove,
itd. Ovakvi programi mogu biti nelogični i mogu lagati.
Drugim riječima funkcioniranje viših razina takvih
programa se ne temelji na logičkoj dedukciji, što
znači da to nisu formalni aksiomatski sustavi, a opet
nisu u kontradikciji s funkcioniranjem njima podložnog hardvera.
S Hofstadterovim protuargumentima, ova rasprava nije završila. Ponovno ju je aktualizirao Roger Penrose (1991) knjigom The Emperor's New Mind, gdje između ostalog, razmatra sposobnosti matematičara koje oni koriste u generiranju novih matematičkih sudova i njihovih dokaza. Po Penroseu, postupak po kojemu matematičar odlučuje o istinitosti novog suda (teorema, formule) ne može se temeljiti na algoritmu ili formalnom sustavu, jer tada bi se odmah moglo Godelovom metodom konstruirati Godelova rečenica i sasvim lako znati da je taj sud istinit i prije njegovog izvođenja. Dakle, matematički uvid nije algoritamski. Također, po njemu ni godelijanski uvid se ne može formalizirati.
Zanimljivi su i zaključci koje Penrose dalje izvlači iz navedene postavke: razmatranjem važnosti fizike za funkcioniranje mozga, on zaključuje da se po našem fizičkom razumijevanju mozgovnih operacija ne može utvrditi ne-algoritamski aspekt uma, pa je dakle, prema modernoj fizici moguće simulirati ljudski um računalom. Otud Penrose zaključuje da moderna fizika mora biti u krivu, tj. da mozak koristi fizičke principe koji još nisu otkriveni, koji moraju biti ne-algoritamski po karakteru te da su vjerojatno povezani s interakcijom kvantne teorije i gravitacije. (Napomena: Penrose je po svojemu obrazovanju fizičar koji je dao značajne rezultate u teoretskoj fizici ; znatno je doprinio otkriću crnih rupa.)
Tu bi bilo zanimljivo spomenuti i jednu vrlo inventivnu ideju
- da se u mozgu odvija kompjutacija i na kvantnoj razini. Ovakvi
nalazi su još uvijek samo teoretski jer ne postoji još
eksperimentalna metoda da se oni provjere. Jibu i Yasue (1997a;
1997b) dokazuju pomoću kvantnih jednadžbi da se u
uvjetima određenih dijelova živčane stanice (naročito
u mikrotubulima) moraju odvijati kvantni procesi koji su povezani
sa spontanim emitiranjem fotona nalik onim kod lasera. Nadalje,
oni sugeriraju da ako je to tako da već na razini jedne
živčane stanice imamo uređaj velike kompjutacijske
snage koji, među ostalim, može utjecati na plastičnost
staničnog prijenosa impulsa. Osim toga oni predlažu
da su kvantne pojave odgovorne za prirodu svijesti.
Ipak, ako se zadržimo na matematičkom aspektu Penroseovih
argumenata, mogu im se uputiti kritike: Prvo, u matematici postoji
duga povijest nekonzistentnosti, krivih teorija, što ukazuje
da su umovi matematičara također podložni ograničenjima.
Skoro svaka važna osoba u povijesti logike je barem jedanput
objavila nekonzistentan skup aksioma (Russel i Norvig, 1995).
Drugo, Penrose ne objašnjava na koji se način godelijanski
uvid ne može formalizirati: možda samim time što
je čovjek uspio dokazati necjelovitost formalnih sustava
je superioran stroju koji to sigurno ne bi mogao izvesti. Ali,
čini se da to nije tako i da je "godelizacija"
u stvari formalizirana. Štoviše, razvijeni su programi
koji automatski dokazuju Godelov teorem iz skupa temeljnih aksioma,
na sličan način kao što je učinio i
sam Godel. Takav je npr. program SHUNYATA, (vidjeti Ammon, 1997).
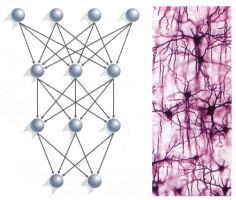
Sredinom 80-ih došlo je do razvoja pristupa kogniciji koji predstavljaju alternativu klasičnim simboličkim pristupima. To su konekcionističke ili neuralne arhitekture koje pomiču naglasak s kompjutacijskih modela na kognitivnu neuroznanost. Takve arhitekture istražuju različite forme ovisnosti sustava o okolinskom kontekstu, složene adaptivne sustave i modele umjetnog života (tzv. artificial life, Alife ili AL) koji su motivirani fenomenima slučajne mutacije i evolucijske selekcije, te sustave interaktivne robotike.
Temeljna strategija konekcionističkog pristupa je da se uzme takva temeljna procesirajuća jedinica koja je bliska apstraktnom neuronu (Rumelhart, 1996). Kompjutacija se tada izvodi paralelno, kroz jednostavne interakcije među takvim neuronima. Ideja je da takvi procesirajući elementi komuniciraju slanjem brojčanih vrijednosti duž linija koje povezuju te elemente. Jedna od osnovnih razlika konekcionističkih modela od onih simboličkih je u ograničenju da se cjelokupno znanje nalazi u vezama među jedinicama. Tako da se vrste veza razlikuju od jednog modela do drugoga. Dakle, znanje je implicitno u strukturi modela koji ga koristi, za razliku od eksplicitnog znanja u simboličkim arhitekturama.
Korištenje ovakvih kompjutacijskih sustava u sustavima nalik onim mozgovnim, ne nudi samo nadu da se opišu načini na koje mozak ustvari izvodi zadatke obrade informacija. Ovakav tip arhitektura nudi i jednostavnije solucije za određene klase problema koje se vrlo teško rješavaju na klasičan, serijski način. Takvi su na primjer problemi najboljeg slaganja ili optimizacije.
Postoji sedam glavnih komponenti svakog konekcionističkog
sustava koji se zajedno nazivaju konekcionistički okvir.
To su:
1) Skup procesirajućih jedinica.
2) Stanje aktivacije definirano nad procesirajućim jedinicama.
3) Izlazna funkcija za svaku jedinicu koja mapira svoje stanje
aktivacije u izlaz.
4) Obrazac povezanosti među jedinicama.
5) Aktivacijsko pravilo za kombiniranje ulaza koji djeluju na
jedinicu s njenim trenutnim stanjem da proizvedu novu razinu
aktivacije za tu jedinicu.
6) Pravilo učenja po kojemu se obrasci povezanosti mijenjaju
s iskustvom.
7) Okolina unutar koje sustav mora operirati.
Konekcionistički modeli se razlikuju od klasičnih
u brojnim dimenzijama (Smith, 1999):
1) Najčešće su paralelni, a ne serijski.
2) Njihovim sastavnim strukturama, naročito u stadiju
dizajniranja, najčešće nije određen nikakav
reprezentacijski ili semantički sadržaj.
3) Takav sadržaj ili interpretacija koja je na kraju određena
se obično temelji na korištenju iskustva, prije nego
čistom denotacijom ili opisom.
4) Ove arhitekture se najčešće koriste za modeliranje
akcije, percepcije, navigacije, motorne kontrole, pokreta tijela
i drugih oblika vezivanja s svijetom, dok se klasične
arhitekture povezane s odvojenim, često deduktivnim zadacima
koji se tiču raznih oblika rješavanja problema i
baratanja znanjem.
5) Konekcionističke arhitekture nastoje da budu "u
realnom vremenu" u smislu zahtjeva za bliskim povezivanjem
trajanja kompjutacijskih procesa i trajanja subjektivne domene.
Visoki prioritet je obično više posvećen i fleksibilnosti i mogućnosti konekcionističke arhitekture da se snalazi s neočekivanim varijacijama u okolini, nego dubokom rezoniranju i čistim deduktivnim vještinama.
Dakle, ove promjene označavaju i promjene u teoretskoj orijentaciji unutar kognitivne znanosti - koje su često opisane u kontrastu s tradicionalnim "kompjutacijskim" pristupima. Ipak, činjenica je da danas ne postoji dovoljno bogata i šire prihvaćena teorija kompjutacije koja može objasniti svu raznolikost u kompjutaciji "stvarnoga svijeta". Prema tome, nije ni jasno mogu li se doista novo predloženi sustavi odrediti kao ne-kompjutacijski. Npr. nitko ne bi mogao reći da ti novi prijedlozi izbjegavaju granice kompjutacijske kompleksnosti koje su postavljene matematičkom teorijom računalne znanosti. Najvjerojatnije se može očekivati da će se pojam "kompjutacije" tako adaptirati da u svoj doseg uvrstiti i te novije pristupe (Smith, 1999).
Kognitivizam koji na kogniciju gleda kao na kompjutaciju u smislu manipulacije diskretnim simbolima je potakao nastanak reakcija na takav pristup koji sebe nazivaju ne- ili čak anti-kompjutacijskim. Takva je dinamička hipoteza o prirodi uma.
Središnja ideja kompjutacijske hipoteze jest da su kognitivni agenti u svojoj osnovi diskretna računala. Prema dinamičkoj hipotezi, kognitivni agenti su dinamički sustavi. Izvjestan utjecaj na ovu hipotezu izvršio je napredak u teoriji dinamičkih sustava, naročito u teoriji nelinearnih sustava i teoriji kaosa. Prema van Gelderovom radu (1998), u kojemu objašnjava i argumentira za dinamičku hipotezu, to znači da kognicija pokazuje određena svojstva dinamičkih sustava. To znači da koriste numeričke varijable, koja imaju svojstva vektora u sustavu.
Dinamička hipoteza uključuje dvije glavne komponente: prirodnu hipotezu i hipotezu znanja.
Prirodna hipoteza je zahtjev o prirodi kognitivnih agenata. Kognitivni su agenti doslovno, identični s dinamičkim sustavima. Hipoteza znanja odnosi se na teoriju kognitivne znanosti. Po njoj bi trebalo cijelu kogniciju shvaćati dinamički. Prema van Gelderu dinamička hipoteza je empirijska hipoteza i kao takva stoji kao čvrsta alternativa kompjutacijskoj hipotezi.
Pokazalo se za rekurentne (povratne) neuralne mreže koje imaju kontinuirani ulaz, dakle, realne, a ne cijele ili racionalne brojeve, da mogu implementirati dinamičke sustave. One se u nekim radovima nazivaju i super-Turingovi automati (npr. Kilian i Siegelmann, 1996; Siegelmann, 1995). Radi se o formalnim strojevima s kompjutacijskom snagom većom od snage Turingovih strojeva, u tom smislu što prepoznaju širu klasu jezika mogu izračunati bilo koju rekurzivnu (Turingovu) funkciju. Dakle, ti su strojevi u svojoj osnovi analogni, a ne diskretni.
Je li pristup koji shvaća kogniciju i adaptivno ponašanje kao dinamički sustav potpuno u suprotnosti s reprezentacijsko-kompjutacijskim shvaćanjima? Van Gelder (1998) smatra da je dinamizam jedini pravi način proučavanja kognicije i odbacuje kompjutacijski pristup. Clarck (1997) naziva takvu, suparničku tezu tezom radikalnog utjelovljenja kognicije, te smatra da se dinamizam lako može pogrešno tumačiti. Nadalje, u istom radu, on obrazlaže da nije zastupnik takve teze, te pokušava pronaći središnju opciju u kojoj se dinamička i kompjutacijska shvaćanja mogu postaviti komplementarno, radije nego suparnički. Konačno, daje zanimljiv prijedlog. Postavlja razliku između tzv. on-line i off-line kognicije i rezoniranja. On-line kognicija se odnosi na akcijski orijentirane karakteristike, u realnom vremenu, u interakciji s okolinom. U to spadaju operacije poput vidne percepcije, motorne kontrole i one su pogodne za opisivanje dinamičkim, dakle konekcionističkim modelima. S druge strane, off-line kognicija nije u realnom vremenu i nije u nužnoj interakciji s okolinom. Ona je reprezentacijska u smislu baratanja znanjem. To su procesi poput dedukcije i oni su pogodni za opisivanje simboličkim, dakle klasičnim kompjutacijskim modelima.
Sličnim idejama o mogućnosti kompatibilnosti dinamičkih pristupa i drugih kognitivnih pristupa raspravljaju i Bechtel (1998), te Wells (1998). Buduća istraživanja bi trebala koristiti i kontinuirane (dinamičke) i diskretne (simboličke) modele da se razumije kognicija, jer nekim kognitivnim kapacitetima bolje odgovaraju jedni, a drugima drugi.
Bez obzira na prijašnju digresiju o alternativnim pogledima na prirodu kognicije i kompjutacije koja nam je poslužila da cjelovitije sagledamo probleme o kojima danas raspravljaju teoretičari kognitivne znanosti, središnje ideje koje želimo istaknuti u ovom tekstu jesu o onoj fascinantnoj složenosti ljudskog uma koji mu omogućuje da se bavi onim problemima koji zadaju toliko briga istraživačima i potiču toliko rasprava. Riječ je o problemima koji u svom temelju imaju postavke halting problema i Godelovog teorema. Dakle, riječ je o ljudskoj intuiciji za beskonačnost.
Kakva je veza između beskonačnosti i navedenih matematičkih formulacija? Takva što bilo koja struktura koja se poziva na samu sebe (koja je rekurzivna) ima mogućnost da se "zavrti" u beskonačnoj petlji. Stvar je još složenija kada se ta struktura negira pozivanjem na sebe. Tada, kako je to već opisano imamo paradoks i nikakvo rješenje se ne može dati. No, tu opet imamo beskonačnu petlju: struktura se negira, onda ta negirana struktura se opet negira čime se afirmira, pa se ta afirmirana i opet negira#133;itd. Ljudi imaju intuiciju o beskonačnosti u smislu da je brzo prepoznaju. Nitko se razmišljajući o rekurzijama neće naći u beskonačnoj petlji ili mu se neće "srušiti sustav" pri pokušaju rješavanja nekog paradoksa. Razlog tome je što je ljudski kognitivni stroj sposoban ne samo izvoditi kompjutaciju, već i kompjutaciju o toj kompjutaciji, i kompjutaciju o kompjutaciji o kompjutaciji, itd. Taj se fenomen u kognitivnoj psihologiji naziva metakognicija.
Metakognicija se (Kellog, 1996) odnosi na kogniciju o kogniciji, ili mišljenje o mišljenju. Ovaj široki pojam uključuje bilo kakvo znanje ili kognitivni proces koji se odnosi, prati ili kontrolira bilo koji aspekt kognicije (Moses i Baird, 1999). Metakognicija sudjeluje u mnogim aspektima kognicije kao što su pažnja, pamćenje, komunikacija, rješavanje problema, te ima važnu primjenu u područjima poput obrazovanja, razvoja i starenja, neuropsihologije te svjedočenja svjedoka. Tijekom kognitivnog razvoja ljudi razvijaju svoje sposobnosti da prate svoje procese mišljenja i da biraju strategije koje su efikasne za zadatak kojim se bave. Istraživanja metakognicije pri rješavanju problema proučavala su razlike među odraslim ekspertima i početnicima i pokazalo se da se značajno razlikuju u metakognitivnim sposobnostima (Kellog, 1996).
Povezani pojam s metakognicijom i koji je na ovom mjestu interesantniji jest metarezoniranje. Metarezoniranje je u najširem smislu "rezoniranje o rezoniranju" (Russell, 1999). To je bilo koji kompjutacijski proces koji se tiče operacija nekog drugog kompjutacijskog procesa unutar istog entiteta. Istraživanja metarezoniranja bila su nerijetko usmjerena na dizajniranje kognitivnih arhitektura koje mogu podržavati introspekciju i refleksiju. Najpoznatija takva arhitektura je SOAR, koja rješava probleme koristeći se i metarazinama (Laird i sur., 1987, prema Russell i Norvig, 1995).
Ipak, nismo naišli na istraživanja i teorije koje se detaljnije bave ljudskim rezoniranjem s beskonačnošću i strategijama koje se koriste pri rješavanju nerješivih problema. Smatramo da bi detaljnije spoznaje o ovoj vrsti ljudskog rezoniranja mogle ponuditi važne smjernice za shvaćanja o prirodi kompjutacije koju izvodi ljudski kognitivni aparat. Konkretno, radilo bi se o ispitivanju ljudske metakognicije i strategija pri suočavanju s problemima koji se ne mogu riješiti, dakle paradoksa. Pojam metakognicije je važan, jer ljudi su sposobni uvidjeti da odgovarajući problemi nisu rješivi, pa i dokazati zašto nisu rješivi.
Konačno, možemo se vratiti na pitanje iz naslova: Kakvi su ljudi kompjutori? Na ovo pitanje još se ne može dati jednostavan odgovor. Kako smo vidjeli postoje ograničenja kompjutacije i još traju rasprave jesu li ljudski umovi podjednako podložni tim ograničenjima. Ograničenje na koje se usredotočio ovaj rad jest matematički argument o ograničenju kompjutacije. Treba napomenuti da to nije jedino pitanje. Postoje tzv. velika pitanja vezana uz kogniciju i nagađa se da li je uopće moguće dati odgovor na njih. To su problem odnosa uma i tijela, problem svijesti, intencionalnosti, qualie itd. (Harman, 1993). Ovi problemi spadaju u filozofski aspekt kognitivne znanosti.
Ovim radom htjelo se kao prvo ukazati na osnovne postavke i karakteristike jedne velike ideje i cjeline - teorije kompjutacije, na čijim se postavkama može računati za opću teoriju kognicije. Pri tome smo se trudili objasniti teorijske specifičnosti koje ove postavke čine problematičnim kada se pokušaju primijeniti na ljudsku kogniciju. Pokazali smo da su te specifičnosti povezane s klasom nerješivih problema - tj. problema za koje se ne može stvoriti algoritamski opis. Nadalje, objasnili smo i neke alternativne pristupe u izučavanju kognicije.
Ideja je da se provede istraživanje iz područja metakognicije, ili preciznije metarezoniranja, u kojem bi se u seriji eksperimenata s različitim nerješivim problemima (i sličnim rješivim zbog kontrolne situacije) pokušale pronaći općenitosti u strategijama koje ljudi koriste. Pri tome bi se pokušale utvrditi zakonitosti na temelju kojih ljudi prepoznaju beskonačnost i nerješiv problem. Bile bi korištene uobičajene opisane metode za ispitivanje rješavanja problema. Na ovaj način bi se moglo prikupiti važan materijal koji bi koristio ne samo u ovom specifičnom području ljudske izvedbe suočene s nerješivim problemima i beskonačnosti, već i u znatno širem razumijevanju ljudske kognicije. Dobiveni rezultati mogli bi poslužiti za konstruiranje algoritma sposobnog da se suočava s nerješivim problemima.
Ammon, K. (1997). An automatic proof of Goedel's
incompleteness theorem. Artificial Intelligence 95: 203-207.
Bechtel, W. (1998). Representations and cognitive explanations:
assesing the dynamicist's challenge in cognitive science. Cognitive
Science 22(3): 295-318.
Clarck, A. (1997). The dynamical challenge. Cognitive Science
21(4): 461-481.
Ćirović, . (1996). Uvod u matematičku logiku
i teoriju rekurzivnih funkcija. Zagreb: Filozosfki niz.
Dietrich, E. (1999). Algorithm. U R. A. Wilson i F. C. Keil (ur.),
The MIT Encyclopedia of the Cognitive Sciences. Cambridge MA:
MIT Press.
Harman, G. (1993). Some philosophical issues in cognitive science:
qualia, intentionaliti, and the mind ; body problem. U M.
I. Posner (Ur.), Foundations of Cognitive Science. Cambridge,
MA: MIT Press.
Hofstadter, D. R. (1980). Goedel, Echer, Bach: An Eternal Golden
Braid. London: Penguin Books.
Hopcroft, J. E., i Ullman, J. D. (1979). Introduction to Automata
Theory, languages and Computation. Addison - Wesley.
Jibu, M., i Yasue, K. (1997a). What is mind? ; Quantum field
theory of evanescent photons in brain as quantum theory of consciousness.
Informatica 21: 471-490.
Jibu, M., i Yasue, K. (1997b). Magic without magic: Meaning of
quantum brain dinamics. The Journal of Mind and Behavior 18(2,3):
205[103] -228[126].
Kilian, J., i Siegelmann, H. T. (1996). The dynamic universality
of sigmoidal neural networks. Information and Computation 128(1):
48-56.
Lucas, J. R. (1961). Minds, machines and Goedel. Philosophy 36:
112-127.
Matuszek, D. (1996). Introduction to the Theory of Computation.
Villanova University.
Moses, L. J., i Baird, J. (1999). Metacognition. U R. A. Wilson
i F. C. Keil (ur.), The MIT Encyclopedia of the Cognitive Sciences.
Cambridge MA: MIT Press.
Penrose, R. (1991). The Emperor's New Mind: Concerning Computers,
Minds and Laws of Physics. New York, NY: Penguin Books.
Podnieks, K. (1992). Around Goedel's Theorem. University of Latvia.
Posner, M. I. (1996). Foundations of Cognitive Science. Cambridge,
MA: MIT Press.
Pylyshyn, Z. W. (1996). Computing in cognitive science. U M.
I. Posner (Ur.), Foundations of Cognitive Science. Cambridge,
MA: MIT Press.
Rumelhart, D. E. (1996). The architecture of mind: a connectionist
approach. U M. I. Posner (Ur.), Foundations of Cognitive Science.
Cambridge, MA: MIT Press.
Russell, S. (1999). Metareasoning. U R. A. Wilson i F. C. Keil
(ur.), The MIT Encyclopedia of the Cognitive Sciences. Cambridge
MA: MIT Press.
Russell, S., i Norvig, P. (1995). Artificial Intelligence: A
Modern Approach. Englewood Cliffs, NJ: Prentice Hall.
Siegelmann, H. T. (1995). Computation beyond Turing limit. Science
268: 545-548.
Simon, H. A. (1991). Primjena kognitivne znanosti u rješavanju
ljudskih problema. U N. N. Šoljan i M. Kovačević
(Ur.), Kognitivna znanost. Zagreb: Školske novine.
Sipser, M. (1997). Introduction to the Theory of Computation.
Boston, MA: PWS Publishing Company.
Smith, B. C. (1999). Computation. U R. A. Wilson i F. C. Keil
(ur.), The MIT Encyclopedia of the Cognitive Sciences. Cambridge
MA: MIT Press.
Turing, A. M. (1936). On computable numbers, with an application
to the Entscheidungsproblem. Proceedings of the London Mathematical
Society 42: 230-265.
Turing, A. M. (1950). Computing machinery and intelligence. Mind
49:433-460.
van Gelder, T. (1998). Dynamical Hypothesis in Cognitive Science.
Behavioral and Brain Sciences 21(5): 615-+
Wells, A. J. (1998). Turing's analysis of computation and theories
of cognitive architecture. Cognitive Science 22(3): 269-294.
Wilson, R. A. i Keil, F. C. (ur.), The MIT Encyclopedia of the
Cognitive Sciences. Cambridge MA: MIT Press.